Gerak Parabola (Perpaduan GLB dan GLBB)-
Perhatikanlah lintasan yang
dibentuk oleh bola basket yang dilemparkan ke dalam ring. Lintasan bola basket
tersebut berbentuk parabola. Gerak yang lintasannya berbentuk parabola disebut
gerak parabola. Contoh umum gerak parabola adalah gerak benda yang dilemparkan
ke atas membentuk sudut tertentu terhadap permukaan tanah. Gerak parabola dapat
dipandang dalam dua arah, yaitu arah vertikal (sumbu-y) yang merupakan
gerak lurus berubah beraturan (GLBB), dan arah horizontal (sumbu-x) yang
merupakan gerak lurus beraturan (GLB). Perhatikan Gambar 1.15 berikut.
Gambar 1.15 Arah
gaya pada lintasan gerak parabola.
Gerak pada sumbu-x (horizontal) adalah gerak lurus
beraturan karena kecepatan benda di setiap titik bernilai konstan dan berlaku
persamaan
vx =
v0x = v0 cos α
Adapun, jarak mendatar yang ditempuh oleh sebuah benda
ditentukan oleh persamaan
x =
vx t = v0cos α t ……… (1–35)
Gerak pada sumbu-y (vertikal) adalah gerak lurus
berubah beraturan, karena benda mengalami perubahan kecepatan akibat percepatan
gravitasi Bumi. Dalam hal ini, arah gerak benda vertikal ke atas sehingga
persamaan kecepatan geraknya pada setiap titik adalah
vy =
v0y – gt ………….. (1–36)
oleh karena v0y = v0
sin α , Persamaan (1–36) dapat dituliskan menjadi
vy =
v0 sin α – gt …………… (1–37)
Posisi benda pada sumbu-y (menurut ketinggian) dapat
dituliskan dengan persamaan berikut
y =
v0y t – ½ gt2 …………….. (1–38)
atau
y =
v0 sin α t – ½gt2 ………….. (1–39)
1. Kecepatan dan Arah Kecepatan Benda di Sembarang Titik
Pada gerak parabola, benda memiliki kecepatan pada komponen
sumbu-x dan sumbu-y sehingga besar kecepatan benda di sembarang
titik secara matematis, dirumuskan sebagai berikut.
Arah kecepatan benda terhadap sumbu mendatar (sumbu-x)
dirumuskan sebagai berikut.
Oleh karena nilai vx selalu positif maka positif atau
negatifnya sudut θ bergantung pada nilai vy.
2. Beberapa Persamaan Khusus pada Gerak Parabola
Persamaan-persamaan khusus gerak parabola ini hanya berlaku
untuk gerak parabola dengan lintasan dari tanah, kemudian kembali lagi ke tanah
seperti pada Gambar 1.16.
Gambar 1.16 Lintasan
gerak parabola benda dengan titik tertinggi di B dan titik terjauh di C.
Pada contoh gerak parabola tersebut, suatu benda bergerak
dari titik A dengan kecepatan awal v0 dan sudut θ . Benda tersebut mencapai
titik tertinggi di titik B dan jarak terjauh di titik C.
a. Waktu untuk Mencapai Titik Tertinggi (Titik B)
Pada saat benda yang melakukan gerak parabola mencapai titik
tertinggi, kecepatan benda pada komponen vertikal (sumbu-y) vy
= 0. Persamaannya adalah sebagai berikut.
vy =
v0y – gtAB
0 = v0 sin α – gtAB
gtAB = v0 sin α
Ketinggian benda di titik tertinggi adalah H = ½ g(tBC)2.
Sifat simetri grafik parabola memperlihatkan bahwa waktu yang diperlukan benda
untuk mencapai titik tertinggi dari posisi awal (tAB), sama dengan waktu
tempuh benda dari titik tertinggi ke jarak terjauh (tBC).
Dengan demikian, akan diperoleh persamaan
b. Tinggi Maksimum (H )
Tinggi maksimum benda yang melakukan gerak parabola dapat
ditentukan dari penurunan Persamaan (1–43) sebagai berikut.
dikuadratkan menjadi
sehingga diperoleh
c. Jarak Terjauh (X )
Waktu tempuh untuk mencapai titik terjauh (titik C) sama
dengan dua kali waktu yang diperlukan untuk mencapai titik tertinggi (tAC
= 2 tAB). Jarak terjauh yang dicapai benda pada sumbu-x (dilambangkan
dengan X) adalah
Menurut trigonometri, 2 sinα cos α = sin 2α sehingga
persamaan untuk jarak terjauh yang dapat dicapai benda dapat dituliskan
Perbandingan antara jarak terjauh (X) dan tinggi
maksimum (H) akan menghasilkan persamaan
Jenis-jenis Gerak Parabola
Dalam kehidupan sehari-hari terdapat beberapa jenis gerak
parabola.
Pertama, gerakan benda berbentuk parabola ketika diberikan
kecepatan awal dengan sudut teta terhadap garis horisontal, sebagaimana tampak
pada gambar di bawah. Dalam kehidupan sehari-hari terdapat banyak gerakan benda
yang berbentuk demikian. Beberapa di antaranya adalah gerakan bola yang
ditendang oleh pemain sepak bola, gerakan bola basket yang dilemparkan ke ke
dalam keranjang, gerakan bola tenis, gerakan bola volly, gerakan lompat jauh
dan gerakan peluru atau rudal yang ditembakan dari permukaan bumi.
Kedua, gerakan benda berbentuk parabola ketika diberikan
kecepatan awal pada ketinggian tertentu dengan arah sejajar horisontal, sebagaimana
tampak pada gambar di bawah. Beberapa contoh gerakan jenis ini yang kita temui
dalam kehidupan sehari-hari, meliputi gerakan bom yang dijatuhkan dari pesawat
atau benda yang dilemparkan ke bawah dari ketinggian tertentu.
Ketiga, gerakan benda berbentuk parabola ketika diberikan
kecepatan awal dari ketinggian tertentu dengan sudut teta terhadap garis
horisontal, sebagaimana tampak pada gambar di bawah.
Menganalisis Gerak Parabola
Gerakan
benda setelah diberikan kecepatan awal pada ketinggian tertentu dengan arah
sejajar horisontal.
Kecepatan awal (vo) gerak benda diwakili
oleh v0x dan v0y.v0x merupakan
kecepatan awal pada sumbu x, sedangkan Kecepatan awal pada sumbu vertikal (voy)
= 0. vy merupakan komponen kecepatan pada sumbu y dan vx merupakan
komponen kecepatan pada sumbu x.
Menganalisis Komponen Gerak Parabola secara terpisah
Sekarang, mari kita turunkan persamaan untuk Gerak Peluru.
Kita nyatakan seluruh hubungan vektor untuk posisi, kecepatan dan percepatan
dengan persamaan terpisah untuk komponen horisontal dan vertikalnya. Gerak
peluru merupakan superposisi atau penggabungan dari dua gerak terpisah tersebut
Komponen kecepatan awal
Terlebih dahulu kita nyatakan kecepatan awal untuk komponen
gerak horisontal v0x dan kecepatan awal untuk
komponen gerak vertikal, v0y.
Catatan : gerak peluru selalu mempunyai kecepatan
awal. Jika tidak ada kecepatan awal maka gerak benda tersebut bukan
termasuk gerak peluru. Walaupun demikian, tidak berarti setiap gerakan yang
mempunyai kecepatan awal termasuk gerak peluru
Karena terdapat sudut yang dibentuk, maka kita harus
memasukan sudut dalam perhitungan kecepatan awal. Mari kita turunkan persamaan
kecepatan awal untuk gerak horisontal (v0x) dan
vertikal (v0y) dengan bantuan rumus Sinus, Cosinus
dan Tangen. Dipahami dulu persamaan sinus, cosinus dan tangen di bawah ini.
Berdasarkan bantuan rumus sinus, cosinus dan tangen di atas,
maka kecepatan awal pada bidang horisontal dan vertikal dapat kita rumuskan
sebagai berikut :
Keterangan : v0 adalah kecepatan awal, v0x adalah
kecepatan awal pada sumbu x, v0y adalah kecepatan awal pada
sumbu y, teta adalah sudut yang dibentuk terhadap sumbu x positip.
Kecepatan dan perpindahan benda pada arah horisontal
Kita tinjau gerak pada arah horisontal atau sumbu x.
Sebagaimana yang telah dikemukakan di atas, gerak pada sumbu x kita analisis
dengan Gerak Lurus Beraturan (GLB). Karena percepatan gravitasi pada arah
horisontal = 0, maka komponen percepatan ax = 0. Huruf x kita
tulis di belakang a (dan besaran lainnya) untuk menunjukkan
bahwa percepatan (atau kecepatan dan jarak) tersebut termasuk
komponen gerak horisontal atau sumbu x. Pada gerak peluru terdapat
kecepatan awal, sehingga kita gantikan v dengan v0.
Dengan demikian, kita akan mendapatkan persamaan Gerak
Peluru untuk sumbu x :
Keterangan : vx adalah kecepatan gerak benda
pada sumbu x, v0x adalah kecepatan awal pada sumbu x, x adalah
posisi benda, t adalah waktu tempuh, x0 adalah posisi awal.
Jika pada contoh suatu gerak peluru tidak diketahui posisi awal, maka silahkan
melenyapkan x0.
Perpindahan horisontal dan vertikal
Kita tinjau gerak pada arah vertikal atau sumbu y.
Untuk gerak pada sumbu y alias vertikal, kita gantikan x dengan y (atau h =
tinggi), v dengan vy, v0 dengan voy dan
a dengan -g (gravitasi). Dengan demikian, kita dapatkan persamaan Gerak Peluru
untuk sumbu y :
Keterangan : vy adalah kecepatan gerak benda pada sumbu y
alias vertikal, v0y adalah kecepatan awal pada sumbu y, g
adalah gravitasi, t adalah waktu tempuh, y adalah posisi benda (bisa juga
ditulis h), y0 adalah posisi awal.
Berdasarkan persamaan kecepatan awal untuk komponen gerak
horisontal v0x dan kecepatan awal untuk komponen
gerak vertikal, v0y yang telah kita turunkan di
atas, maka kita dapat menulis persamaan Gerak Peluru secara lengkap sebagai
berikut :
Setelah menganalisis gerak peluru secara terpisah, baik pada
komponen horisontal alias sumbu x dan komponen vertikal alias sumbu y, sekarang
kita menggabungkan kedua komponen tersebut menjadi satu kesatuan. Hal ini membantu
kita dalam menganalisis Gerak Peluru secara keseluruhan, baik ditinjau dari
posisi, kecepatan dan waktu tempuh benda. Pada pokok bahasan Vektor dan Skalar
telah dijelaskan teknik dasar metode analitis. Sebaiknya anda mempelajarinya
terlebih dahulu apabila belum memahami dengan baik.
Persamaan untuk menghitung posisi dan kecepatan resultan
dapat dirumuskan sebagai berikut.
Pertama,
vx tidak pernah berubah sepanjang lintasan, karena setelah
diberi kecepatan awal, gerakan benda sepenuhnya bergantung pada gravitasi. Nah,
gravitasi hanya bekerja pada arah vertikal, tidak horisontal. Dengan demikian vx bernilai
tetap.
Kedua,
pada titik tertinggi lintasan, kecepatan gerak benda pada bidang vertikal alias
vy = 0. pada titik tertinggi, benda tersebut hendak kembali
ke permukaan tanah, sehingga yang bekerja hanya kecepatan horisontal alias vx,
sedangkan vy bernilai nol. Walaupun kecepatan vertikal (vy) =
0, percepatan gravitasi tetap bekerja alias tidak nol, karena benda tersebut
masih bergerak ke permukaan tanah akibat tarikan gravitasi. jika gravitasi nol
maka benda tersebut akan tetap melayang di udara, tetapi kenyataannya tidak
teradi seperti itu.
Ketiga, kecepatan
pada saat sebelum menyentuh lantai biasanya tidak nol.





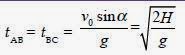














Tidak ada komentar:
Posting Komentar